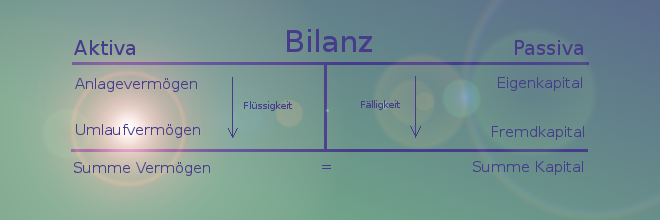
In der Bilanz wird das Vermögen dem Kapital eines Unternehmens gegenübergestellt. Diese Darstellung erfolgt in Form eines Kontos. Hierbei wird die linke Seite als Aktiva und die rechte Seite als Passiva bezeichnet. Auf der Aktivseite werden die Vermögenswerte aufgelistet und auf der Passivseite das Kapital.
Bilanz: Was steht drin und wonach wird es geordnet?
Dabei wird das Vermögen aufgegliedert in das Anlagevermögen und das Umlaufvermögen. Das Kapital wird unterteilt in das Eigenkapital und das Fremdkapital. Unter dem Begriff Fremdkapital werden sämtliche Schulden aufgelistet.
Die einzelnen Posten des Vermögens werden nach ihrer Flüssigkeit geordnet. Die Posten des Kapitals werden nach ihrer Fälligkeit geordnet.
Mit Flüssigkeit ist die Liquidität gemeint, das heißt wie schnell der Vermögensposten in Bargeld umgewandelt werden kann. Je schneller das geht, umso höher ist seine Flüssigkeit.
Mit Fälligkeit ist gemeint, wann diese Schuld zurück gezahlt werden muss. (Wann ist sie fällig?, Wie lange kann das Unternehmen noch mit diesem Kapital arbeiten, bevor es zurückgezahlt werden muss?)
Bilanz: Was ist die Bilanzsumme und was hat das mit dem Eigenkapital zu tun?
Am Ende der Bilanz wird auf jeder Seite die Summe ausgewiesen: Am Ende der Aktiva steht die Summe des Vermögens. Am Ende der Passiva befindet sich die Summe des Kapitals. Die Summe der beiden Seiten ist immer gleich. Das nennt man Bilanzsumme.
Das Wort Bilanz ist übrigens vom italienischen bilancia abgeleitet, was Waage bedeutet. Damit ist eben dieser Zustand gemeint, dass sich Aktiva (Vermögen) und Passiva (Kapital) die Waage halten, also in ihrer Summe gleich sind:
Umlaufvermögen + Anlagevermögen = Eigenkapital + Fremdkapital
Aus der Bilanzsumme folgt, dass sich das Eigenkapital ergibt, wenn man das Fremdkapital vom gesamten Vermögen abzieht:
Umlaufvermögen + Anlagevermögen – Fremdkapital = Eigenkapital
oder
Vermögen – Schulden = Eigenkapital
Somit ergibt sich das Eigenkapital in der Bilanz (auch) als Saldo.
Bilanz: Wie lange ist die Aufbewahrungsfrist?
Die Bilanz ist 10 Jahre lang aufzubewahren.
Du möchtest noch mehr verständliche Erklärungen zu Buchführungsthemen inklusive Übungen und Lösungen?
Dann hol dir jetzt das E-Book „Fit in Buchführung“!






